Question

Suppose a revenue function is given by: R ( q ) = − q 3 + 140 q where q is thousands of units and R ( q ) is thousands of dollars. For what value of q is revenue maximized. Round your answer to the nearest tenth (one decimal place). q = Incorrect thousand units

Answer 1

At q=6.8 the revenue is maximum. So, q=6.8 thousand units.

Explanation:

The revenue function is

`R(q)=-q^3+140q`

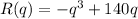
where q is thousands of units and R ( q ) is thousands of dollars.

We need to find for what value of q is revenue maximized.

Differentiate the function with respect to q.

`R'(q)=-3q^2+140`

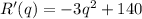
Equate R'(q)=0, to find the critical values.

`0=-3q^2+140`

`3q^2=140`

Divide both sides by 3.

`q^2=(140)/(3)`

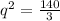
Taking square root both the sides.

`q=\pm \sqrt{(140)/(3)}`

`q=\pm 6.8313`

`q\approx \pm 6.8`

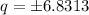
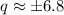
Find double derivative of the function.

`R''(q)=-6q`

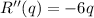
For q=-6.8, R''(q)>0 and q=6.8, R''(q)<0. So at q=6.8 revenue is maximum.

At q=6.8 the revenue is maximum. So, q=6.8 thousand units.