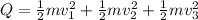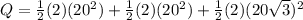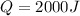Question

A 6.0-kg object, initially at rest in free space, "explodes" into three segments of equal mass. Two of these segments are observed to be moving with equal speeds of 20 m/s with an angle of 60° between their directions of motion. How much kinetic energy is released in this explosion?

Answer 1

`Q = 2000 J`

Step-by-step explanation:

As we know that the 6 kg object was at rest initially

So here since net force on the system is zero

so the momentum of the system will always remains conserved

so we can say

`0 = P_1 + P_2 + P_3`

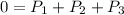
now we know that

`P_1 = P_2 = P`

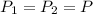
and the angle between the two objects is 60 degree

so we can say

`\vec P_1 + \vec P_2 = √(P_1^2 + P_2^2 + 2P_1 P_2cos60)`

`\vec P_1 + \vec P_2 = √(P^2 + P^2 + 2P^2(0.5)) = \sqrt3 P`

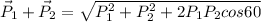
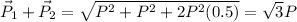
now we can say that the speed of the third mass will be

`v_3 = \sqrt 3 (20) m/s`

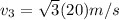
now the total kinetic energy released in this system is given as

`Q = (1)/(2)mv_1^2 + (1)/(2)mv_2^2 + (1)/(2)mv_3^2`

`Q = (1)/(2)(2)(20^2) + (1)/(2)(2)(20^2) + (1)/(2)(2)(20\sqrt3)^2`

`Q = 2000 J`