Answer:

Explanation:
we know that
In a Geometric Sequence each term is found by multiplying the previous term by a constant, called the common ratio (r)
In this problem we have

Remember that
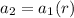 ----->
----->
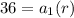 -----> equation A
-----> equation A
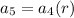
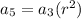
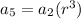
Substitute the values of a_5 and a_2 and solve for r
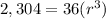
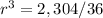
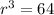
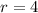
Find the value of a_1 in equation A
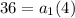
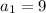
therefore
The explicit rule for the nth term is
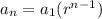
substitute
