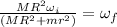Question

A disk of mass m and radius r is initially held at rest just above a larger disk of mass M and radius R that is rotating at angular speed ωi. What is the final angular speed of the disks after the top one is dropped onto the bottom one and they stop slipping on each other?

Answer 1

`(MR^(2)\omega _(i))/((MR^(2)+mr^(2)))=\omega _(f)`

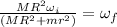
Step-by-step explanation:

Mass of small disc = m

radius of small disc = r

Mass of large disc = M

Radius of large disc = R

Initial angular speed = ωi

Let the final angular speed is ωf

As no external torque of applied on the system so the angular system remains constant.

I1 ωi = I2 ωf

MR^2 ωi = (MR^2 + mr^2) ωf

`MR^(2)\omega _(i)=(MR^(2)+mr^(2))\omega _(f)`

`(MR^(2)\omega _(i))/((MR^(2)+mr^(2)))=\omega _(f)`