Question

At noon, ship A is 50 nautical miles due west of ship B. Ship A is sailing west at 22 knots and ship B is sailing north at 20 knots. How fast (in knots) is the distance between the ships changing at 5 PM? (Note: 1 knot is a speed of 1 nautical mile per hour.)

Answer 1

distance between the ships changing 29.255 knot

Step-by-step explanation:

Given data

time = noon to 5 pm = 5 hours

A = 50 nautical miles due west of B

A = sailing west at 22 knots

B = sailing north at 20 knots

to find out

How fast is the distance between the ships changing

solution

we consider a to b distance is z and at noon ship at 90 degree angle of AB at x and y distance from AB respectively

so here z² = x² + y² ..............1

and 2z z' = 2x x' + 2y y'

so z' = ( x x' + y y' ) / z

and after 5 hours

x = 50 + 22(t) = 50 + 22(5) = 160

y = 20(t) = 20 (5) = 100

so from equation 1

z² = x² + y²

z² = 160² + 100²

z =
`√(25600+10000)`

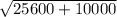
z = 188.68

so z' = ( x x' + y y' ) / z

z' = ( 160 (22) + 100(20) ) / 188.68

z' = 29.255

distance between the ships changing 29.255 knot