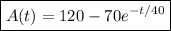Question

A tank contains 120 liters of fluid in which 50 grams of salt is dissolved. Brine containing 1 gram of salt per liter is then pumped into the tank at a rate of 3 L/min; the well-mixed solution is pumped out at the same rate. Find the number A(t) of grams of salt in the tank at time t.

Answer 1

If A(t) is the amount of salt in the tank at time t, then A(0) = 50 g and

A'(t) = (1 g/L)*(3 L/min) - (A(t)/120 g/L)*(3 L/min)

`\implies A'+\frac A{40}=3`

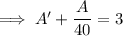
Multiply both sides by
`e^(t/40)`, so that the left side can be condensed as the derivative of a product:

`e^(t/40)A'+(e^(t/40))/(40)A=3e^(t/40)`

`\left(e^(t/40)A\right)'=3e^(t/40)`

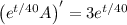
Integrate both sides and solve for A(t).

`e^(t/40)A=120e^(t/40)+C`

`\implies A(t)=120+Ce^(-t/40)`

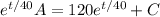
Given that A(0) = 50 g, we have

`50=120+C\implies C=-70`

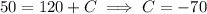
so that the amount of salt in the tank at time t is

`\boxed{A(t)=120-70e^(-t/40)}`