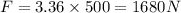Question

A particular satellite with a mass of m is put into orbit around Ganymede (the largest moon of Jupiter) at a distance 300 km from the surface. What is the gravitational force of attraction between the satellite and the moon? (Ganymede has a mass of 1.48x1023 kg and a radius of 2631 km.)

Answer 1

3.36m or 1680 N

Step-by-step explanation:

Given:

Mass of the satellite =m

Mass of the moon Ganymede, M = 1.48 × 10²³ kg

Radius of Ganymede, R = 2631 km

Distance of satellite above the surface of the moon, d = 300 km

According to Universal Gravitational law:

`F=(GMm)/((R+d)^2)`

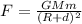
where, G is the gravitational constant, M and m are mass of the objects and (R+d) is the distance between the centers of the objects.

Substitute the values:

`F=(6.67* 10^(-11)* 1.48 * 10^(23) m)/((2.931* 10^6)^2)=3.36m`

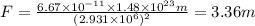
If we consider mass of a satellite to be about 500 kg, the gravitational force between the moon and the satellite would be:

`F = 3.36* 500 = 1680 N`