Question

The crate, which sets on a 10 degree incline, has a weight of 3433.5 N and is subjected to a towing force P acting at a 20 degree angle with the horizontal. If the coefficient of static friction is µs = 0.5, determine the force P needed to just start the crate moving down the plane.

Answer 1

P = 981 N

Step-by-step explanation:

Given

Angle of the incline θ = 10°

Angle of the towing force φ =20°

Weight of the crate W = 3433.5 N

The coefficient of static friction µ = 0.5

Solution

Forces Acting along the ramp

`\mu N = Pcos(10^(o)+10^(o))+Wsin10^(0) \\\mu N = Pcos30^(o)+Wsin10^(0)`

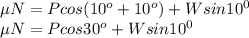
Forces acting perpendicular to the ramp

`N + Psin30^(o)=Wcos10^(0)\\\\N=Wcos10^(0)-Psin30^(o)\\`

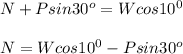
Substituting the value of N we get

`\mu[Wcos10^(0)-Psin30^(o)] =Pcos30^(o)+Wsin10^(0)\\\\\mu Wcos10^(0)- \mu Psin30^(o) =Pcos30^(o)+Wsin10^(0)\\\\\mu Wcos10^(0)- Wsin10^(0)=Pcos30^(o)+\mu Psin30^(o) \\\\P=W(\mu cos10^(0)- sin10^(0))/(cos30^(o)+\mu sin30^(o)) \\\\P=3433.5(0.5 * cos10^(0)- sin10^(0))/(cos30^(o)+0.5 *  sin30^(o))\\\\P=980.66\\\\ P = 981 N`