Answer:
$16.125≅ $16.13
Step-by-step explanation:
in the question
Correlation coefficient β doubles
we know that
Required return= risk free return + (market risk premium)*β
0.13= 0.05 + 0.07*β
β= 1.1428
current β of 1.1428
now
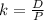
where
k= expected return
D= expected dividend after the end of the year
P= current market prize per share
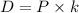
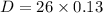 =3.38
=3.38
so current dividend is $3.38 per share
now, when β doubles it become 2.28
hence required return = 0.05 +0.07*2.28
= 0.2096
=20.96%
The dividend remains the same D= $3.38
now
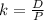
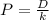

=$16.125
so, when the β doubles, the prize of the market per share becomes $16.125