Question

A process capability study is conducted for an injection mold. You are tasked to evaluate if the process will yield a greater than 99% acceptance relative to the critical dimension assigned to you. The part requires 1.45” +/-0.008 and you are given 20 parts that measure an average of 1.45” with a standard deviation of 0.0015. What is the range of the true mean with 99% confidence interval?

Answer 1

Answer: 1.4494 and 1.4506

Explanation:

Given : Sample size :
`n=20`, which is less than 30 so the sample is a small sample.

Sample mean :
`\overline{x}=1.45`

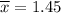
Standard deviation :
`\sigma= 0.0015`

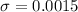
Significance level :
`\alpha=1-0.99=0.01`

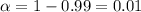
Critical value :
`t_(n-1,\alpha/2)=t_(19,0.005)=1.729`

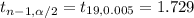
The confidence interval for population mean is given by :-

`\mu\ \pm t_(n-1,\alpha/2)(\sigma)/(√(n))`

`=1.45\pm(1.729)(0.0015)/(√(20))\\\\\approx1.45\pm0.0006\\\\=(1.45-0.0006,\ 1.45+0.0006)=(1.4494,\ 1.4506)`

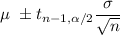
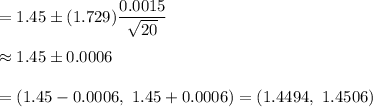
Hence, the range of the true mean with 99% confidence interval is between 1.4494 and 1.4506.