Question

It is a well-known fact that 50% of the general population are rascals (P(R) = 0.5) and 50% of the general population are not rascals (P(RC ) = 0.5). Furthermore, scientists have determined that about 90% of rascals wear a top hat at all times, while only 30% of non-rascals wear top hats.

Suppose that you meet a person who is wearing a top hat. Given the information that they are wearing a top hat, what is the probability that they are a rascal?

A. 0.09
B. 0.45
C. 0.6
D. 0.75

Answer 1

The answer is D. 0.75

Explanation:

Let call R the event that a person is rascal, RC a person is not rascal, TH a person use top hat and NTH a person don’t use top hat.

From the information on the question we have 4 options with their respective probability:

1. A person could be rascal and use top Hat: this probability is calculate as the multiplication of the probability of be a rascal (0.5) and use a top hat (0.9), then:

P(R y TH)=0.5*0.9=0.45

2. A person could be rascal and don’t use top Hat: this probability is calculate as the multiplication of the probability of be a rascal (0.5) and not use a top hat (0.9), then:

P(R y NTH)=0.5*0.1=0.05

3. A person could be not rascal and use top Hat: this probability is calculate as the multiplication of the probability of not be a rascal (0.5) and use a top hat (0.3), then:

P(RC y TH)=0.5*0.3=0.15

4. A person could be not rascal and not use top Hat: this probability is calculate as the multiplication of the probability of not be a rascal (0.5) and not use a top hat (0.7), then:

P(RC y NTH)=0.5*0.7=0.35

Then the probability that a person is a rascal given that he is wearing a top hat could be written and calculate as:

`P(R/TH)=(P(R y TH))/(P(TH))`

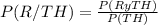
For calculate P(TH) we need to sum all the option in which TH is involve so:

P(TH) = P(R y TH)+ P(RC y TH)

P(TH)=0.45+0.15=0.6

Replacing values on the first equation we get:

`P(R/TH)=(0.45)/(0.6) =0.75`

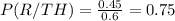
So, the probability that a person is a rascal given that he is wearing a top hat is 0.75