Question

The magnitude and direction exerted by two tugboats towing a ship are 1670 ​kilograms, N30degrees​W, and 1250 ​kilograms, S60degrees​W, respectively. Find the​ magnitude, in​ kilograms, and the direction​ angle, in​ degrees, of the resultant force.

Answer 1

magnitude=2085.99 kg

direction angle= 23.18°

Step-by-step explanation:

let the forces be x,y

x = 1670cos(90°+30°) i +1670sin(90°+30°) j,

y = 1250cos(-90°-60°) i +1250sin(-90°-60°) j

x = 1670cos(120°) i + 1670sin(120°) j,

y = 1250cos(-150°) i + 1250sin(-150°) j

resultant force = x+y

resultant force = 1670cos(120°) i +1670sin(120°) j + 1250cos(-150°) i +1250sin(-150°) j

taking i and j term together

resultant force = (1670cos(120°) +1250cos(-150°)) i +(1670sin(120°) +1250sin(-150°)) j

resultant force = -1917.53 i +821.26j

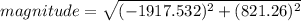
`magnitude=\sqrt {(-1917.532)^(2) + (821.26)^(2)}`

magnitude=2085.99 kg

direction angle=
`tan^(-1)((821.26)/(1917.53))`

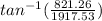
direction angle= 23.18°