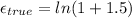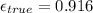Question

1 Rubber specimens, having an initial length of 5 cm, are tested, one in compression and one in tension. If the engineering strains are −1.5 and +1.5, respectively, what will be the final lengths of the specimens? What are the true strains, and why are they numerically different?

Answer 1

We know that

`Strain=(L_(f)-L_(o))/(L_(o))`

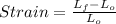
For specimen in compression we have engineering strain is -1.5 which is not possible since a item cannot compress more than it's initial length

2)

For item in tension we have

`1.5=(L_(f)-5)/(5)\\\\\therefore L_(f)=1.5* 5+5\\L_(f)=12.5cm`

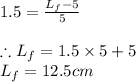
3) the true strain are obtained when we use the actual area of the specimen in calculating stress in the specimen which decreases due to poission effect and necking and not the initial nominal area. The true strain is related to engineering strain as

`\epsilon _(true)=ln(1+\epsilon _(engg))`

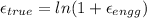
Applying values

For specimen in tension we have

`\epsilon _(true)=ln(1+1.5)`

`\epsilon _(true)=0.916`