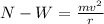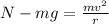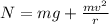Answer:
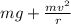
Step-by-step explanation:
At the bottom of the pipe :
 = Normal force acting in upward direction
= Normal force acting in upward direction
 = mass of the ball
= mass of the ball
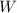 = weight of the ball acting in downward direction = mg
= weight of the ball acting in downward direction = mg
 = speed of the ball at the bottom
= speed of the ball at the bottom
 = radius of curvature
= radius of curvature
Force equation for the motion of ball is given as