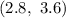Question

How much sugar do reduced sugar cookies typically have? You take a random sample of 51 reduced-sugar cookies and test them in a lab, finding a mean sugar content of 3.2 grams and a standard deviation of 1.1 grams of sugar. Create a 99% confidence interval for the mean grams of sugar.

Answer 1

Answer:
`(2.8,\ 3.6)`

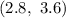
Explanation:

The confidence interval for population mean is given by :-

`\overline{x}\pm z_(\alpha/2)(\sigma)/(√(n))`

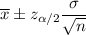
Given : Sample size : n= 51 ( >30 , that means its a large sample)

Sample mean :
`\overlien{x}=3.2\text{ grams}`

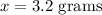
Standard deviation :
`\sigma=1.1\text{ grams}`

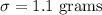
Significance level :
`1-0.99=0.01`

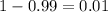
Critical value :
`z_(\alpha/2)=\pm2.576`

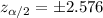
Now, the 99% confidence interval for the mean grams of sugar will be :-

`=3.2\pm(2.576)*(1.1)/(√(51))\\\\\approx3.2\pm0.40\\\\=(2.8,\ 3.6)`

Hence, the 99% confidence interval for the mean grams of sugar
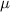`\mu` =
`(2.8,\ 3.6)`