Answer:
30 mi/h
Explanation:
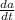 = Velocity of car A = 24 mi/h
= Velocity of car A = 24 mi/h
a = Distance car A travels in 3 hours = 24×3 = 72 mi
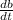 = Velocity of car B = 18 mi/h
= Velocity of car B = 18 mi/h
b = Distance car B travels in 3 hours = 18×3 = 54 mi
c = Distance between A and B after 3 hours = √(a²+b²) = √(72²+54²) = 90 mi
From pythogoras theorem
a²+b² = c²
Now, differenciating with respect to time
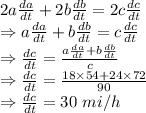
∴ Rate at which distance between the cars is increasing three hours later is 30 mi/h