Answer:
a)
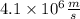
b)
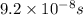
c)

d) 175000 volts
Step-by-step explanation:
a)
 = magnitude of charge on the alpha particle = 2 x 1.6 x 10⁻¹⁹ C = 3.2 x 10⁻¹⁹ C
= magnitude of charge on the alpha particle = 2 x 1.6 x 10⁻¹⁹ C = 3.2 x 10⁻¹⁹ C
 = mass of alpha particle = 4 x 1.67 x 10⁻²⁷ kg = 6.68 x 10⁻²⁷ kg
= mass of alpha particle = 4 x 1.67 x 10⁻²⁷ kg = 6.68 x 10⁻²⁷ kg
 = radius of circular path = 5.99 cm = 0.0599 m
= radius of circular path = 5.99 cm = 0.0599 m
 = magnitude of magnetic field = 1.43 T
= magnitude of magnetic field = 1.43 T
 = speed of the particle
= speed of the particle
Radius of circular path is given as
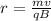
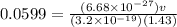
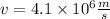
b)
Time period is given as

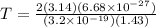

c)
Kinetic energy is given as

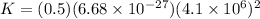
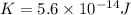
d)
ΔV = potential difference
Using conservation of energy
q ΔV = K
(3.2 x 10⁻¹⁹) ΔV = 5.6 x 10⁻¹⁴
ΔV = 175000 volts