Question

A ball is thrown horizontally from the top of a 64.5-m building and lands 103.8 m from the base of the building. Ignore air resistance. (Assume the ball is thrown in the +x direction and upward to be in the +y direction.) How long (in s) is the ball in the air?

Answer 1

The ball is in the air for 3.628 sec

Step-by-step explanation:

We can find speed in the "y" direction when the ball lands with this equation:

`V_(fy) ^(2) = V_(oy) ^(2) + 2*g*(y_(f) - y_(o))`

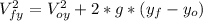
Where:
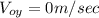`V_(oy) = 0 m/sec` because the ball is thrown horizontally

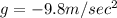`g = - 9.8 m/sec^(2)` because gravity is a vector that points down in the "y" direction

`y_(o) = 64.5 m`

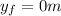`y_(f) = 0 m` because the ball lands on the ground

Then:
`V_(fy) ^(2) = (0 m/sec)^(2) + 2(-9.8 m/sec^(2))(0 m - 64.5 m)`

`V_(fy) ^(2) = 2(- 9.8 m/sec^(2))(- 64.5 m)`

`V_(fy) ^(2) = 1264.2 m^(2)/sec^(2)`

`V_(fy) = \sqrt{1264.2 m^(2)/sec^(2)}`

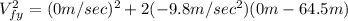
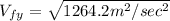
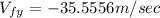`V_(fy) = - 35.5556 m/sec` because the ball is falling and that means speed in the "y" direction is a vector that points down

Now we can calculate the time with next equation:

`V_(fy) = V_(oy) + g*t`

`V_(fy) - V_(oy) = g*t`

`t = (V_(fy) - V_(oy))/(g)`

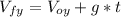
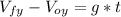
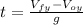
Then:
`t = (-35.5556 m/sec - 0 m/sec)/(- 9.8 m/sec^(2))`

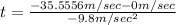
Finally t = 3.628 sec