Question

What is the radius of a tightly wound solenoid of circular cross-section that has 180turns if a change in its internal magnetic field of 3.0 T/s causes a 6.0 A current to flow?The resistance of the circuit that contains the solenoid is 17 ȍ. The only emf source forthe circuit is the induced emf.

Answer 1

Radius of cross section, r = 0.24 m

Step-by-step explanation:

It is given that,

Number of turns, N = 180

Change in magnetic field,
`(dB)/(dt)=3\ T/s`

Current, I = 6 A

Resistance of the solenoid, R = 17 ohms

We need to find the radius of the solenoid (r). We know that emf is given by :

`E=N(d\phi)/(dt)`

`E=N(d(BA))/(dt)`

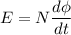
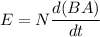
Since, E = IR

`IR=NA(dB)/(dt)`

`A=(IR)/(N.(dB)/(dt))`

`A=(6\ A* 17\ \Omega)/(180* 3\ T/s)`

`A=0.188\ m^2`

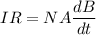
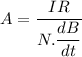
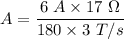
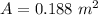
or

`A=0.19\ m^2`

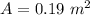
Area of circular cross section is,
`A=\pi r^2`

`r=\sqrt{(A)/(\pi)}`

`r=\sqrt{(0.19)/(\pi)}`

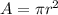
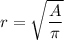
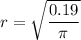
r = 0.24 m

So, the radius of a tightly wound solenoid of circular cross-section is 0.24 meters. Hence, this is the required solution.