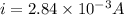Question

The magnitude J of the current density in a certain wire with a circular cross section of radius R = 2.11 mm is given by J = (3.25 × 108)r2, with J in amperes per square meter and radial distance r in meters. What is the current through the outer section bounded by r = 0.921R and r = R?

Answer 1

`i = 2.84 * 10^(-3) A`

Step-by-step explanation:

As we know that current density is ratio of current and area of the crossection

now we have

`J = (di)/(dA)`

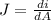
so the current through the wire is given as

`i = \int J dA`

now we have

`i = \int_(0.921R)^R J dA`

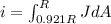
here we have

`J = (3.25 * 10^8)r^2`

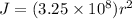
now plug in the values in above equation

`i = \int_(0.921R)^R (3.25 * 10^8)r^2 2\pi r dr`

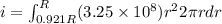
now we have

`i = \int_(0.921R)^R 2\pi (3.25 * 10^8)r^3 dr`

`i = (2.04 * 10^9) (r^4)/(4)`

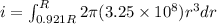
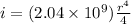
now plug in both limits as mentioned

`i = (2.04 * 10^9)((R^4)/(4) - ((0.921R)^4)/(4))`

`i = (2.04* 10^9)(0.07 R^4)`

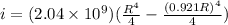
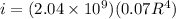
here R = 2.11 mm

`i = (2.04 * 10^9)(0.07 (2.11 * 10^(-3))^4)`

`i = 2.84 * 10^(-3) A`