Answer:
A. 5.82%
B. 16.11%
C. 54.93%
D. 29.42%
Explanation:
First draw the normal distribution curve for the situation as in the attached image. The middle line is the mean(μ) of 99.7, and every line away from the middle is a standard deviation(σ) of 20 more or less. Next calculate the z-score for each scenario. The z-score basically calculates how many standard deviations, the number in question is, from the mean.
Z-Scores:
The formula to calculate a z-score is as follows:
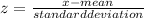
A:
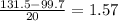
B:
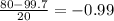
C:
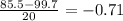
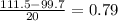
D:
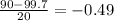
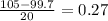
Convert Z scores to percentiles:
Use the attached tables to convert z scores to percentiles. The tables are in decimals, so multiply by 100 to find percentile, and note that percentages are given to the left of the vertical line.
A: 94.18 % to the left of the line, which is less than 131.50, thus 5.82% is more.
B: 16.11 % is less than 80.
C: 23.89 % is less than 85.50
78.52% is less than 115.50
Between 85.50 and 115.50 can be calculated as
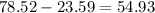
D: 31.21 % is less than 90
60.64% is less than 105
Between 85.50 and 115.50 can be calculated as
