Answer:
v = 4.17 m/s
Step-by-step explanation:
as we know that block is moving towards the end of the rod
so let say just after the collision the block is moving with speed v' and rod is rotating with speed "w"
so we have angular momentum conservation about the hinge point
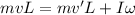
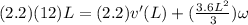
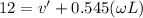
now by the equation of coefficient of restitution we can say
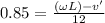
now we have

now we have
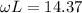
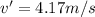
so velocity of block just after collision is 4.17 m/s