Question

The trace of a square matrix A is the sum of the diagonal entries in A and is denoted by tr A. It can be verified that ​tr(FG)equals​tr(GF) for any two n times n matrices F and G. Show that if A and B are​ similar, then tr Upper A equals tr Upper B.

Answer 1

Answer with Step-by-step explanation:

We are given that tr(FG)=tr(GF) for any two matrix of order
`n* n`

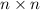
We have to show that if A and B are similar then

tr upper A=tr upper B

Trace of a square matrix A is the sum of diagonal entries in A and denoted by tr A

We are given that A and B are similar matrix then there exist a inverse matrix P such that

Then
`B=P^(-1)AP`

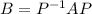
Let
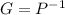`G=P^(-1)` and F=AP

Then
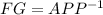`FG= APP^(-1)`=A

GF=
`P^(-1)AP=B`

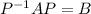
We are given that tr(FG)=tr(GF)

Therefore, tr upper A=trB

Hence, proved