a. The inverse of d(r) is r(d) = (d + 90.39)/6.97.
b. It has been verified that these are inverse functions.
c. If the distance required to stop was 300 feet, the predicted speed of the car is 56.01 miles per hour.
In this exercise, we have to determine the inverse of the square function f(x). This ultimately implies that, we would have to interchange both the independent value (x-value) and dependent value (y-value) as follows;
d(r) = 6.97r - 90.39
By interchanging d and r, we have:
r = 6.97d - 90.39
r + 90.39 = 6.97d
d = (r + 90.39)/6.97
By replacing d with r(d), we have:
r(d) = (d + 90.39)/6.97
Part b.
In order to verify that r = r(d) is the inverse of d = d(r), we would have to evaluate both compositions to see that r(d(r)) = r and d(r(d)) = d;
r(d(r)) = r(6.97r − 90.39)
r(d(r)) = [(6.97r − 90.39) + 90.39]/6.97
r(d(r)) = 6.97r/6.97
r(d(r)) = r.
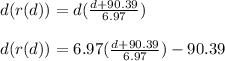
d(r(d)) = (d + 90.39) - 90.39
d(r(d)) = d
Part c.
Since the distance required to stop was 300 feet, the predicted speed of the car can be calculated as follows;
r(d) = (d + 90.39)/6.97
r(d) = (300 + 90.39)/6.97
r(d) = 390.39/6.97
r(d) = 56.01 miles per hour.
Complete Question;
Taking into account reaction time, the distance d in feet that a car requires to come to a complete stop while travelingr miles per hour is given by the following function.
d(r) = 6.97r - 90.39
a. Find the inverse of d (r), written r(d).
b. Verify that r = r(d) is the inverse of d = d(r) by showing that r(d(r)) = r and d(r(d)) = d.
c. Predict the speed that a car was traveling if the distance required to stop was 300 feet.