Question

An oil layer that is 5.0 cm thick is spread smoothly and evenly over the surface of water on a windless day. A light ray from the air above enters the oil at 45° with the normal and then goes into the water. What is the angle of refraction of this ray in the water? The index of refraction for the oil is 1.15, and for water it is 1.33.

Answer 1

The angle of refraction in water 32.12°.

Step-by-step explanation:

Given that,

Thickness = 5.0 cm

Index of refraction for oil = 1.15

Index of refraction for water = 1.33

Angle = 45°

We need to calculate the angle of refraction

When the ray of light enters from air to oil

Using formula of refraction

`n_(a)\sin\theta_(a)=n_(o)\sin\theta_(o)`

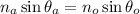
Where,
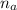`n_(a)` = refractive index of air

`n_(0)` = refractive index of oil

Put the value into the formula

`1*\sin45=1.15\sin\theta_(o)`

`\sin\theta_(o)=(1)/(√(2)*1.15)`

`\sin\theta_(o)=0.6148`

`\theta_(o)=sin^(-1)0.6149`

`\theta_(o)=37.94^(\circ)`

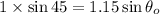
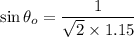
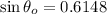
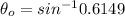
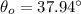
When the ray of light enters from oil to water

Using formula of refraction

`n_(0)\sin\theta_(0)=n_(w)\sin\theta_(w)`

Where,
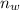`n_(w)` = refractive index of water

`1.15*\sin37.94^(\circ)=1.33\sin\theta_(w)`

`\sin\theta_(w)=(1.15\sin37.94^(\circ))/(1.33)`

`\theta_(w)=\sin^(-1)0.53163`

`\theta_(w)=32.12^(\circ)`

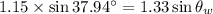
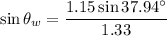
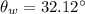
Hence, The angle of refraction in water 32.12°.