Answer:
The probability of choosing mathematics =P(M)=
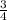
The probability that he chooses either art or French=1
Explanation:
We are given that a student must choose exactly two out of three elective subjects : art ,french and mathematics.
The probability of choosing art=
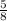
The probability of choosing french =
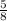
The probability of choosing French and art=
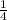
Let A ,F and M denotes the students of art,french and mathematics.
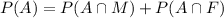
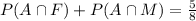
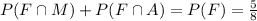
Probability of choosing mathematics only=0
Probability of choosing French only =0
Probability of choosing art only =0
Probability of choosing all three subjects =0
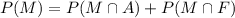
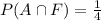
Substitute the value then we get
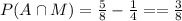
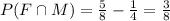
Therefore,
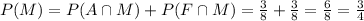
Hence, the probability of choosing mathematics =P(M)=
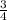
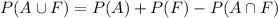
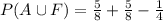
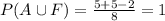
Hence, the probability that he chooses either art or French=1