Step-by-step explanation:
It is given that,
Mass of the block, m = 3 kg
Initially, the block is at rest, u = 0
Force acting on the block, P = 12 N
The coefficient of kinetic friction between the block and the surface is,
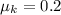
We need to find the rate is the force P doing work on the block at t = 2.0 s. The rate at which work is done is called the power. Let is equal to P'
Frictional force acting on the block,
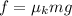
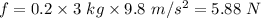
So, the net force acting on the block, F = P - f
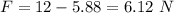
Let a is the acceleration of the block,
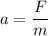
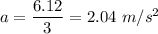
Let v is the velocity of the block after 2 seconds. So,


v = 4.08 m/s
Power,
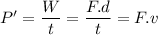
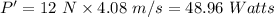
So, the force P is doing work on the block at the rate of 48.96 watts.