Question

A simple random sample of size nequals40 is drawn from a population. The sample mean is found to be 104.3​, and the sample standard deviation is found to be 18.2. Is the population mean greater than 100 at the alphaequals0.01 level of​ significance?

Answer 1

We conclude that population mean is equal to 100 at the α=0.01 level of​ significance.

Explanation:

Given information:

Sample size, n=40

Sample mean=104.3

sample standard deviation, s=18.2

We need to check whether the population mean greater than 100 at the α=0.01 level of​ significance.

Null hypothesis:

`H_0:\mu=100`

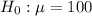
Alternative hypothesis:

`H_1:\mu>100`

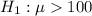
Let as assume that the data follow the normal distribution. It is a right tailed test.

The formula for z score is

`z=\frac{\overline{x}-\mu}{(s)/(√(n))}`

`z=(104.3-100)/((18.2)/(√(40)))`

`z=1.494263`

`z\approx 1.49`

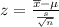
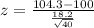
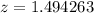
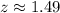
Using the standard normal table the p-value at z=1.49 and 0.01 level of significance is 0.068112.

(0.068112 > 0.01) p-value is greater than α, so we accept the null hypothesis.

Therefore, we conclude that population mean is equal to 100 at the α=0.01 level of​ significance.