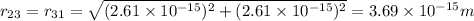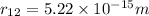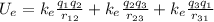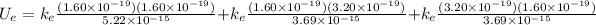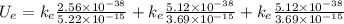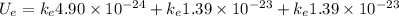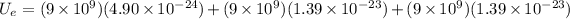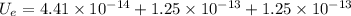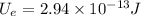Answer:
(a)
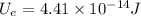
(b)
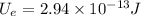
Explanation:
(a)The formula for the electric potential energy is:
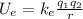
Where
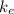 is the Coulomb's constant and is equal to
is the Coulomb's constant and is equal to
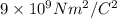 ,
,
 and
and
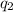 are the charges and
are the charges and
 is the distance between them. In this case
is the distance between them. In this case
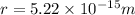 ,
,
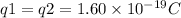 .
.
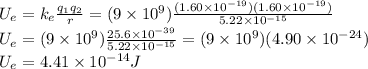
(b) In systems with three charges, the electric potential energy is the sum of the contribution made by each pair of the charges, i.e. the electric potential energy of the charges
 and
and
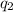 plus the electric potential energy of the charges
plus the electric potential energy of the charges
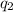 and
and
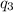 plus the electric potential energy of the charges
plus the electric potential energy of the charges
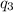 and
and
 .
.
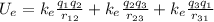
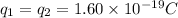
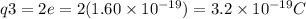
Since
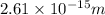 is half of
is half of
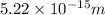 , the charge
, the charge
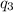 is at the same distance from
is at the same distance from
 as from
as from
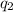 and is the hypotenuse of the triangle rectangle with two equal sides of
and is the hypotenuse of the triangle rectangle with two equal sides of
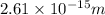 .
.