Question

The GMAC Insurance company reported that the mean score on the National Drivers Test was 69.9 with a standard deviation of 3.3 points. The test scores are approximately bell-shaped. Approximately 68% of all test scores were between two values A and B. What is the value of A? Write only a number as your answer. Round to one decimal place.

Answer 1

Answer: The value of A is 66.6.

Explanation:

According to the Empirical rule ,

Approximately 68% of all data values lies within one standard deviation from the mean.

Given : The GMAC Insurance company reported that the mean score on the National Drivers Test was 69.9 with a standard deviation of 3.3 points.

The test scores are approximately bell-shaped.

Then , Approximately 68% of all test scores were between 69.9- 3.3 and 69.9+3.3.

i.e. Approximately 68% of all test scores were between 66.6 and 73.2 .

On comparing it to the statement, "Approximately 68% of all test scores were between two values A and B. "

Hence, the value of A is 66.6.

Answer 2

The value of A is 66.6.

Explanation:

Consider the provided information.

The mean score on the National Drivers Test was 69.9 with a standard deviation of 3.3 points.

It is given that the test scores are approximately bell-shaped and approximately 68% of all test scores were between two values A and B.

Therefore, the probability is 0.68,

The standard deviation
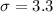`\sigma=3.3` and
`\mu=69.9`

To find the value of A use the formula:
`A=\mu-\sigma`

Substitute the respective values in above formula.

`A=69.9-3.3`

`A=66.6`

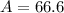
Hence, the value of A is 66.6.

Similarly, we can find the value of B as:
`B=\mu+\sigma`

`B=69.9+3.3`

`B=73.2`

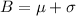
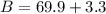
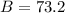
The value of B is 73.2.

The true mean value lies between 66.6 and 73.2.