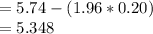Answer:
(
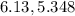 )
)
Explanation:
Given -
Mean of the sample (μ)
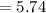
Standard error (SE)
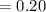
Significance level is equal to
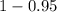
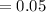
Critical value for this significance level
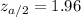
Now the confidence interval for the population mean number of hours spent per week on the internet is given by
μ

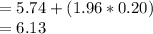
μ