Question

The following hypotheses are given. H0 : σ1² = σ2² H1 : σ1² ≠ σ2² A random sample of eight observations from the first population resulted in a standard deviation of 10. A random sample of six observations from the second population resulted in a standard deviation of 7.

1. State the decision rule for 0.02 significance level. (Round your answer to 1 decimal place.) Reject H0 if F >
2. Compute the value of the test statistic. (Round your answer to 2 decimal places.)
3. At the 0.02 significance level, is there a difference in the variation of the two populations?
__________H0. There is ______ in the variations of the two populations

Answer 1

Explanation:

From the question; for 0.02 level and
`n_1 -1 = 7` ;
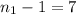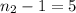`n_2 -1 = 5`; degree of freedom.

The critical value (F) = 0.1340 and 10.4555

Decision rule: reject
`H_o` if test statistic
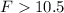`F>10.5` ( to one decimal place) or
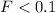`F<0.1` ( to on decimal place)

Test statistic:

`F = ((s_1)/(s_2))^2 \\ \\ = ((10)/(7))^2 \\ \\`

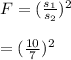
= 2.0408

= 2.04 (to two decimal place)

As test statistic does not fall into critical region we can not reject null hypothesis.

Conclusion:

Accept
`H_o` .There is significant variations of the two population.

Answer 2

Explanation:

This is a two tailed test for comparison of two variances at 2% significance level

`n_1 = 8:  n_2 =6\\s_1 =10: s_2 = 7`

deg of freedom = 7

F statistic =
`(s_1^2)/(s_2^2) =(100)/(49) \\=2.041`

p value = 0.4496

1. State the decision rule for 0.02 significance level. (Round your answer to 1 decimal place.) Reject H0 if F >10.4555

2.F=2.041

3. _Accept_________H0. There is __no significant____ in the variations of the two populations