Question

A battery-operated car utilizes a 12.0 V system. Find the charge (in C) the batteries must be able to move in order to accelerate the 850 kg car from rest to 25.0 m/s, make it climb a 2.30 ✕ 102 m high hill, and then cause it to travel at a constant 25.0 m/s by exerting a 4.00 ✕ 102 N force for an hour.

Answer 1

The required charge is 3.175 × 10⁶ C

Step-by-step explanation:

Given:

Potential difference, ΔV = 12.0 V

mass of the car (m) = 850 kg

velocity of the car, v = 25.0 m/s

Height of the hill upto which car traveled, h = 2.3 × 10² m = 230 m

Now, the energy required to accelerate the car from rest to 25 m/s will be

E₁ = kinetic energy of the car =
`(1)/(2)mv^2`

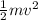
on substituting the values we get

E₁ =
`(1)/(2)850* 25^2`

or

E₁ = 2.65 × 10⁵ J

Now, the potential energy gained by the car at the height 'h' will be

E₂ = mgh = 850 × 9.8 × 230 = 1.91 × 10⁶ J

Also, the energy required to make the car travel at the constant speed of 25.0 m/s with the force of 4 × 10² N for an hour will be

W = Force × displacement

now, the displacement will be = velocity × time = 25 m/s × 1hr = 25 × 3600 = 90000 m [as 1 hr = 3600 seconds]

substituting in the above equation, we get

W = 4.0 × 10² N × 90000 m = 36 × 10⁶ J

Now, the electric potential energy (ΔU) is given as:

ΔU = qΔV

where, q is the charge

Now this electric potential energy is required to do all the work in the above cases

thus,

ΔU = E₁ + E₂ + W

or

qΔV = E₁ + E₂ + W

on substituting the values in the above equation, we get

q × 12 = 2.65 × 10⁵ J + 1.91 × 10⁶ J + 36 × 10⁶ J

or

q = (3.81 × 10⁷)/12

or

q = 3.175 × 10⁶ C

Hence, the required charge is 3.175 × 10⁶ C