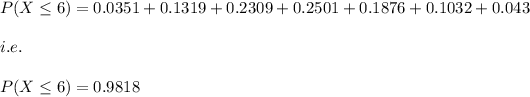Answer:
The probability is:
0.9818
Explanation:
We need to use the binomial theorem in order to find the probability.
We know that when there are r successes out of n total experiments such that p denote the probability of success then the probability of r successes is given by the formula:
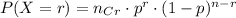
Here we khave:
n=15
p=0.20
Hence,
1-p=1-0.20=0.80
Also, we are asked to find the probability that the number of correct answers is at most 6 i.e.
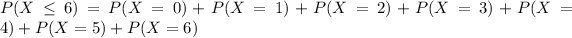
![P(X=0)=15_C_0\cdot (0.20)^(0)\cdot (0.80)^(15-0)\\\\i.e.\\\\P(X=1)=1\cdot 1\cdot (0.80)^(15)\\\\i.e.\\\\P(X=1)=0.0351</p><ul><li></li></ul><p>[tex]P(X=1)=15_C_1\cdot (0.20)^(1)\cdot (0.80)^(15-1)\\\\i.e.\\\\P(X=1)=15\cdot (0.20)\cdot (0.80)^(14)\\\\i.e.\\\\P(X=1)=0.1319](https://img.qammunity.org/2020/formulas/mathematics/high-school/834699ywzft5jfewrmoi49zx14r89imi6z.png)
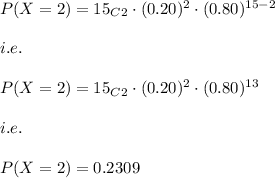
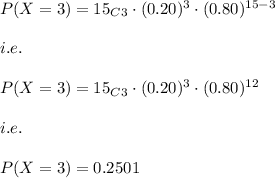
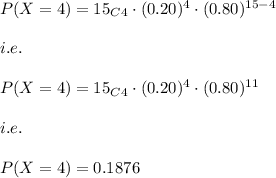
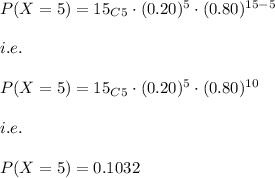
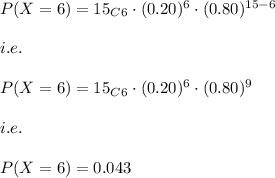
Hence,