Question

Grains of fine California beach sand are approximately spheres with an average radius of 50 μm and are made of silicon dioxide, which has a density of 2.5 × 103 kg/m3. What mass of sand grains would have a total surface area (the total area of all the individual spheres) equal to the surface area of a cube 1.1 m on an edge?

Answer 1

0.30042 kg = 300.42 gram

Step-by-step explanation:

Given data:

Density, D = 2.5 × 10³ kg/m³

Radius, r = 50 μm = 50 × 10⁻⁶ m³

edge of the cube, a = 1.1 m

Now, Mass (M) is given as :

M = Density × Volume

M =
`2.5*10^3*((4)/(3)\pi r^3)`

or

M =
`2.5*10^3*((4)/(3)\pi (50*10^(-6))^3)`

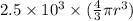
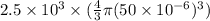
or

M = 1.30 × 10⁻⁹ Kg

Thus, the mass of single sand grain is 1.30 × 10⁻⁹ Kg

Now, the number of grains required for the 1.1 m edge cube total surface area

the surface area of the cube = number of sand grains (n) × (surface area of the single sand grain)

6 × a² = n × 4πr²

on substituting the values

we have

6 × 1.1² = n × 4 × π × (50 × 10⁻⁶)²

n = 231.092 × 10⁶

Thus, the mass of the sand required will be = n × M = 231.092 × 10⁶ × 1.30 × 10⁻⁹ Kg = 0.30042 kg = 300.42 gram