Question

What is the velocity of a proton that has been accelerated by a potential difference of 15 kV? (i)\:\:\:\:\:9.5\:\times\:10^5\:m.s^{-1} ( i ) 9.5 × 10 5 m . s − 1 (ii)\:\:\:\:2.2\:\times\:10^9\:m.s^{-1} ( i i ) 2.2 × 10 9 m . s − 1 (iii)\:\:\:3.9\:\times\:10^8\:m.s^{-1} ( i i i ) 3.9 × 10 8 m . s − 1 (iv)\:\:\:\:1.7\:\times\:10^6\:m.s^{-1}

Answer 1

Velocity of a proton,
`v=1.7* 10^6\ m/s`

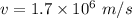
Step-by-step explanation:

It is given that,

Potential difference,
`V=15\ kV=15* 10^3\ V`

Let v is the velocity of a proton that has been accelerated by a potential difference of 15 kV.

Using the conservation of energy as :

`(1)/(2)mv^2=qV`

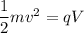
q is the charge of proton

m is the mass of proton

`v=\sqrt{(2qV)/(m)}`

`v=\sqrt{(2* 1.6* 10^(-19)\ C* 15* 10^3\ V)/(1.67* 10^(-27)\ kg)`

`v=1695361.75\ m/s`

`v=1.69* 10^6\ m/s`

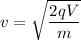
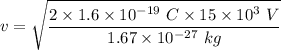
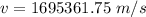
or

`v=1.7* 10^6\ m/s`

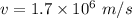
So, the velocity of a proton is
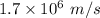`1.7* 10^6\ m/s`. Hence, this is the required solution.