Question

An optical disk drive in your computer can spin a disk up to 10,000 rpm (about 1045 rad/s1045 rad/s ). If a particular disk is spun at 646.1 rad/s646.1 rad/s while it is being read, and then is allowed to come to rest over 0.234 seconds0.234 seconds , what is the magnitude of the average angular acceleration of the disk?

Answer 1

The magnitude of the average angular acceleration of the disk is 2761.1 rad/s².

Step-by-step explanation:

Given that,

Angular velocity of optical disk= 1045 rad/s

Angular velocity of particular disk = 646.1 rad/s

Time = 0.234 sec

We need to calculate the average angular acceleration

Using formula of angular acceleration

`\alpha=(\omega_(f)-\omega_(i))/(t)`

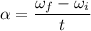
Where,
`\omega_(f)` = final angular velocity

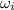`\omega_(i)` = Initial angular velocity

t = time

Put the value in the equation

`\alpha = (0-646.1)/(0.234)`

`\alpha= -2761.1\ rad/s^2`

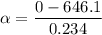
Negative sign shows the angular deceleration.

Hence, The magnitude of the average angular acceleration of the disk is 2761.1 rad/s².