Question

A soft drink (mostly water) flows in a pipe at a beverage plant with a mass flow rate that would fill 220 0.355 - L cans per minute. At point 2 in the pipe, the gauge pressure is 152kPa and the cross-sectional area is 8.00cm2. At point 1, 1.35m above point 2, the cross-sectional area is 2.00cm2.

a) Find the mass flow rate.
b) Find the volume flow rate.
c) Find the flow speeds at points 1 and 2.
d) Find the guage pressure at point 1.

Answer 1

a) 1.301 kg/s

b) 0.001301 m³/s

c) V₁ = 6.505 m/s, V₂ = 1.626 m/s

d) 118.93 kPa

Step-by-step explanation:

Given:

The number of cans = 220

The volume of can, V = 0.355 L = 0.355 × 10⁻³ m³

time = 1 minute = 60 seconds

gauge pressure at point 2, P₂ = 152 kPa

b) Thus, the volume flow rate, Q = Volume/ time

Q = (220 × 0.355 × 10⁻³)/60 = 0.001301 m³/s

a) mass flow rate = Volume flow rate × density

since it is mostly water, thus density of the drink = 1000 kg/m³

thus,

mass flow rate = 0.001301 m³/s × 1000 kg/m³ = 1.301 kg/s

c) Given:

Cross section at point 1 = 2.0 cm² = 2 × 10 ⁻⁴ m²

Cross section at point 2 = 8.0 cm² = 8 × 10 ⁻⁴ m²

also,

Q = Area × Velocity

thus, for point 1

0.001301 m³/s = 2 × 10 ⁻⁴ m² × velocity at point 1 (V₁)

or

V₁ = 6.505 m/s

for point 2

0.001301 m³/s = 8 × 10 ⁻⁴ m² × velocity at point 1 (V₂)

or

V₂ = 1.626 m/s

d) Applying the Bernoulli's theorem between the points 1 and 2 we have

`P_1+\rho gV_1 + (\rho V_1^2)/(2)=P_2+\rho gV_2 + (\rho V_2^2)/(2)`

or

`P_1=P_2+\rho*g(y_2-y_1)+(\rho)/(2)(V_2^2-V_1^2))`

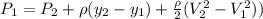
on substituting the values in the above equation, we get

`P_1=152+1000* 9.8(1.35)+(1000)/(2)(1.626^2-6.505^2))`

it is given that point 1 is above point 2 thus, y₂ -y₁ is negative

or

`P_1=118.93\ kPa`

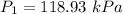
thus, gauge pressure at point 1 is 118.93 kPa