Question

Use the normal distribution to find a confidence interval for a proportion p given the relevant sample results. Give the best point estimate for p, the margin of error, and the confidence interval. Assume the results come from a random sample. A 90% confidence interval for p given that p Overscript ^ EndScripts equals 0.7 and n equals 110.

Answer 1

Answer: (0.63, 7.07)

Explanation:

The confidence interval for population proportion is given by :-

`\hat{p}\pm z_(\alpha/2)\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}`

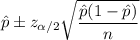
Given :
`\hat{p} =0.7` ;
`n=110`

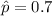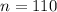
Significance level :
`1-0.90=0.1`

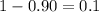
Critical value :
`z_(\alpha/2)=1.645`

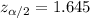
Now, a 90% confidence interval for population proportion will be :-

`0.7\pm (1.645)\sqrt{(0.7(1-0.7))/(110)}\\\\\approx0.7\pm0.07\\\\=(0.7-0.07,0.7+0.07)=(0.63,\ 7.07)`

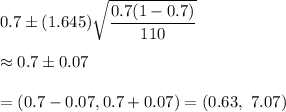
Hence, a 90% confidence interval for population proportion = (0.63, 7.07)