Question

When a certain tree was first planted, it was 4 feet tall, and the height of the tree increased by a constant amount each year for the next 6 years. At the end of the 6th year, the tree was 1/5 taller than it was at the end of the 4th year. By how many feet did the height of the tree increase each year?

Answer 1

`(2)/(3)\text{ feet}`

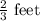
Explanation:

Let the equation that models the height of the tree after x years,

y = mx + c

Where, m is constant amount of increasing and c is any constant,

Given,

When x = 0, y = 4,

⇒ 4 = m(0) + c ⇒ c = 4,

Now, the height of plant after 4th year = m(4) + c = 4m + c

Also, the height of plant after 6th year = m(6) + c = 6m + c

According to the question,

6m + c is
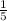`(1)/(5)` more than 4m + c,

`6m+c=4m+c + (1)/(5)(4m+c)`

`6m+c = (6)/(5)(4m+c)`

`30m+5c=24m+6c`

`6m=c`

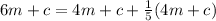
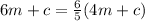
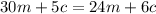
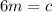
By substituting the value of c

6m = 4

⇒
`m=(4)/(6)=(2)/(3)`

Hence, 2/3 feet of height is increased each year.