Question

Explain the correspondence that lets us easily translate between linear motion and rotational motion. What are the linear analogues of the rotational quantities we have discussed in lecture (i.e. angle, angular velocity, angular acceleration, moment of inertia)? Where does the correspondence seem to fail?

Answer 1

Step-by-step explanation:

The linear analog of angle is angle itself.

The linear analog of angular velocity is linear velocity.

ω is angular velocity, therefore linear velocity is given by v

∴ for linear velocity,
`v^(2) = u^(2)+2.a.S`

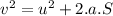
for angular velocity,
`\omega_(f)^(2)  = \omega _(i)^(2)+2.a.S`

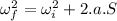
The linear analog of angular acceleration is acceleration.

α is angular acceleration whereas as a is linear acceleration.

∴ for linear acceleration, v = u + a.t

for angular acceleration,
`\omega_(f)= \omega _(i)+\alpha .t`

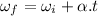
The linear analog of moment of inertia is mass.

I is moment of inertia and m is mass,

∴ for linear analog, F = m.a

for angular analog, τ - I.α