Question

If there are x teams in a sports​ league, and all the teams play each other​ twice, a total of​ N(x) games are​ played, where ​N(x)equalsxsquaredminusx. A softball league has 5 ​teams, each of which play the others twice. If the league pays ​$35 per​ game, how much will it cost to play the entire​ schedule?

Answer 1

It will cost $700 to play the entire​ schedule.

Explanation:

Given :
`N(x)=x^2-x`

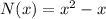
To Find : A softball league has 5 ​teams, each of which play the others twice. If the league pays ​$35 per​ game, how much will it cost to play the entire​ schedule?

Solution:

Equation for total no. of games when all the teams play each other​ twice is
`N(x)=x^2-x`

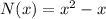
Now we are given that A softball league has 5 ​teams, each of which play the others twice.

So, Substitute x = 5 in the given equation

`N(x)=5^2-5`

`N(x)=20`

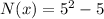
So, The total no. of games = 20

Cost for 1 game = $35

So, cost for 20 games =
`35 * 20 = 700`

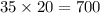
Hence it will cost $700 to play the entire​ schedule.