Question

Find the magnitude of the electric field at points along the axis of a dipole (along the same line that contains +Q and −Q) for r≫ℓ, where r is the distance from a point to the center of the dipole and ℓ is the distance between +Q and −Q.

Answer 1

E=
`(2K\cdot P)/(r^3)`

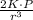
Step-by-step explanation:

We are given that a dipole consist of two charge Q and -Q and charge separated by l.Let a charge +1 C is placed at point P at distance r from the centre of dipole.

We have to find the magnitude of the electric field at point along the axis of dipole .

We know that Electric field=
`(Force)/(unit \;positive\;Charge)`

Electric filed due to positive charge Q

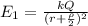`E_1=(kQ)/((r+(\rho)/(2))^2)` {from A to P}

Electric field due to negative charge -Q

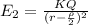`E_2=(KQ)/((r-(\rho)/(2))^2)` ( Along PB)

Net electric field E=
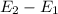
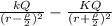
`E_2-E_1`

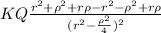
E=
`(kQ)/((r-(\rho)/(2))^2)-(KQ)/((r+(\rho)/(2))^2)`

E=
`KQ(r^2+\rho^2+r\rho-r^2-\rho^2+r\rho)/((r^2-(\rho^2)/(4))^2)`

E=
`(2 KQ r\rho)/((r^2-(\rho^2)/(4))^2)`

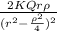
We are given that r >> L then

E=
`(2KQ r\rho)/(r^4)=(2kQ \rho)/(r^3)`

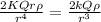
E=
`(K\cdot 2Q\rho)/(r^3)`

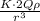
E=
`(2K\cdot P)/(r^3)`

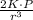
Where, P=Diple = Distance between two charges
`*` any charge