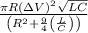Question

A resistor R, inductor L, and capacitor C are connected in series to an AC source of rms voltage ΔV and variable frequency. If the operating frequency is twice the resonance frequency, find the energy delivered to the circuit during one period. (Use the following as necessary: the rms voltage ΔV, R, L, and C.)

Answer 1

Answer:E=
`(\pi R\left ( \Delta V\right )^2√(LC))/(\left ( R^2+(9)/(4)\left ((L)/(C) \right )\right ))`

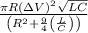
Step-by-step explanation:

We know resonant frequency is given by

`\omega_0=(1)/(√(LC))`

and the operating frequency is given by

`\omega =2\omega_0=(2)/(√(LC))`

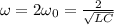
The capacitance reactance is given by

`X_c=(1)/(\omega C)=(√(LC))/(2C)=(1)/(2)\sqrt{(L)/(C)}`

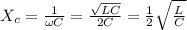
inductive reactance is given by

`X_L=\omega L=\left ( (2)/(√(LC))\right )L=2\sqrt{(L)/(C)}`

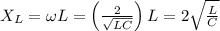
Thus impedance is

`Z=\left ( R^2+\left (X_L-X_C \right )^2 \right )^(1)/(2)`

`Z=\left ( R^2+\left (2\sqrt{(L)/(C)}-(1)/(2)\sqrt{(L)/(C)} \right )^2 \right )^(1)/(2)`

`Z=\left ( R^2+(9)/(4)\left ( (L)/(C) \right ) \right )^(1)/(2)`

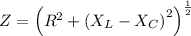
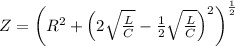
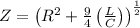
The average power delivered is

`P_(avg.)=(\Delta V^2)/(Z)cos\phi =(\left ( \Delta V\right )^2)/(Z)\left ((R)/(Z) \right )`

`P_(avg.)=(\left (\Delta V \right )^2R)/(\left ( R^2+(9)/(4)\left ((L)/(C) \right )\right ))`

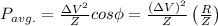
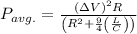
Energy Delivered in one cycle is given by

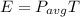
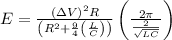
`E=P_(avg)T`

`E=(\left (\Delta V \right )^2R)/(\left ( R^2+(9)/(4)\left ((L)/(C) \right )\right ))\left ( (2\pi )/((2)/(√(LC)))\right )`

E=
`(\pi R\left ( \Delta V\right )^2√(LC))/(\left ( R^2+(9)/(4)\left ((L)/(C) \right )\right ))`