Answer:
The probability that M produces a word that looks like a byte is
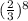 .
.
Step-by-step explanation:
It is given that a message source M of a digital communication system outputs a word of length 8 characters.
The characters drawn from the ternary alphabet {0,1,2}, and all such words are equally probable.
Total possible outcomes is
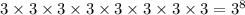
We need to find the probability that M produces a word that looks like a byte (i.e., no appearance of ‘2’). It means only 0 and 1 are included in the word.
Total favorable outcomes is
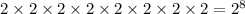
The formula for probability is

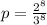
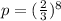
Therefore the probability that M produces a word that looks like a byte is
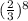 .
.