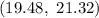Question

A senior student researches to estimate the time taken by applicants to fill out an application form for college admissions. Fifty randomly selected students were timed as they filled out the form. The time required had mean of 20.4 minutes with a standard deviation of 2.1 minutes. Construct a 99.8% confidence interval for the mean time taken for all students to fill out the form.

Answer 1

Answer:
`(19.48,\ 21.32)`

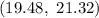
Explanation:

The confidence interval for population mean is given by :-

`\mu\ \pm z_(\alpha/2)(\sigma)/(√(n))`

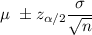
Given : Sample size :
`n=50`

`\mu=20.4\text{ minutes}`

`\sigma=2.1\text{ minutes}`

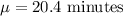
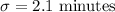
Significance level :
`1-0.99.8=0.002`

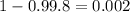
Critical value :
`z_(\alpha/2)=3.090`

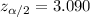
Now, the 99.8% confidence interval for the mean time taken for all students to fill out the form will be :-

`20.4\ \pm (3.09)(2.1)/(√(50))\\\\\approx20.4\pm0.92\\\\=(19.48,\ 21.32)`

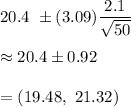
Hence, a 99.8% confidence interval for the mean time taken for all students to fill out the form =
`(19.48,\ 21.32)`