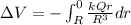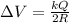Question

A solid sphere of radius R carries charge Q distributed uniformly throughout its volume. Find the potential difference from the sphere's surface to its center. Express your answer in terms of the variables R, Q and Coulomb constant k.

Answer 1

`\Delta V = (kQ)/(2R)`

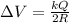
Step-by-step explanation:

As we know that electric field inside the solid sphere is given by

`E = (kQr)/(R^3)`

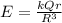
here we know that

Q = total charge on the sphere

R = radius of the sphere

r = distance from the center of the sphere

now by the relation of potential difference and electric field we know that

`\Delta V = -\int E. dr`

now for the potential difference between centre and the surface we have

`\Delta V = -\int_R^0 (kQr)/(R^3) dr`

`\Delta V = (kQ)/(2R)`