Question

Assume that the red blood cell counts of women are normally distributed with a mean of 4.577 million cells per microliter and a standard deviation of 0.382 million cells per microliter. Approximately what percentage of women have red blood cell counts in the normal range from 4.2 to 5.4 million cells per​ microliter? Round to two decimal places. A. ​16.11% B. ​17.69% C. ​82.26% D. ​4.09%

Answer 1

Answer: C. ​82.26%

Step-by-step explanation:

Given : The red blood cell counts of women are normally distributed with

`\mu=4.577\text{ million cells per microliter}`

`\sigma=0.382\text{ million cells per microliter}`

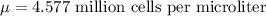
Let X be the random variable that represents the red blood cell counts of randomly selected woman.

Z-score :
`z=(X-\mu)/(\sigma)`

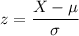
For X=4.2

`z=(4.2-4.577)/(0.382)\approx-0.99`

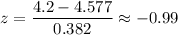
For X=5.4

`z=(5.4-4.577)/(0.382)\approx2.1544`

Now, the probability that the women have red blood cell counts in the normal range from 4.2 to 5.4 million cells per​ microliter will be :-

`P(4.2<X<5.4)=P(-0.99<z<2.15)\\\\=P(z<2.1544)-P(z<-0.99)\\\\=0.9843955-0.1618458=0.8225497\approx0.8226=82.26\%`

Hence, 82.26% of women have red blood cell counts in the normal range from 4.2 to 5.4 million cells per​ microliter.