Question

Suppose 4.00 mol of an ideal gas undergoes a reversible isothermal expansion from volume V1 to volume V2 = 9V1 at temperature T = 240 K. Find (a) the work done by the gas and (b) the entropy change of the gas. (c) If the expansion is reversible and adiabatic instead of isothermal, what is the entropy change of the gas?

Answer 1

(a) The work done by the gas on the surroundings is, 17537.016 J

(b) The entropy change of the gas is, 73.0709 J/K

(c) The entropy change of the gas is equal to zero.

Step-by-step explanation:

(a) The expression used for work done in reversible isothermal expansion will be,

`w=nRT\ln ((V_2)/(V_1))`

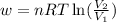
where,

w = work done = ?

n = number of moles of gas = 4 mole

R = gas constant = 8.314 J/mole K

T = temperature of gas = 240 K

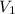`V_1` = initial volume of gas =
`V_1`

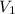
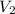`V_2` = final volume of gas =
`9V_1`

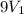
Now put all the given values in the above formula, we get:

`w=4mole* 8.314J/moleK* 240K* \ln ((9V_1)/(V_1))`

`w=17537.016J`

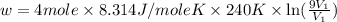
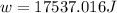
The work done by the gas on the surroundings is, 17537.016 J

(b) Now we have to calculate the entropy change of the gas.

As per first law of thermodynamic,

`\Delta U=q-w`

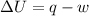
where,

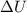`\Delta U` = internal energy

q = heat

w = work done

As we know that, the term internal energy is the depend on the temperature and the process is isothermal that means at constant temperature.

So, at constant temperature the internal energy is equal to zero.

`q=w`

Thus, w = q = 17537.016 J

Formula used for entropy change:

`\Delta S=(q)/(T)`

`\Delta S=(17537.016J)/(240K)=73.0709J/K`

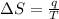
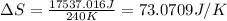
The entropy change of the gas is, 73.0709 J/K

(c) Now we have to calculate the entropy change of the gas when the expansion is reversible and adiabatic instead of isothermal.

As we know that, in adiabatic process there is no heat exchange between the system and surroundings. That means, q = constant = 0

So, from this we conclude that the entropy change of the gas must also be equal to zero.