Answer:
Let the initial velocity of this projectile be
 .
.
If the object is launched at an angle of projection
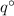 ,
,
Time of the object in the air:
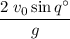 ;
;
Horizontal range:
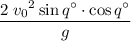 .
.
If the object is launched at an angle of projection
 ,
,
Time of the object in the air:
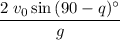 ;
;
Horizontal range:
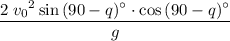 .
.
However
 and
and
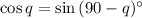 .
.
Therefore
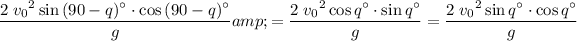 .
.
Hence the horizontal range of the projectile will be the same if the object is launched at an angle of projection
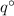 and at
and at

Step-by-step explanation:
Let the initial velocity of this projectile be
 . If this projectile is launched at an angle of elevation of
. If this projectile is launched at an angle of elevation of
 , the horizontal velocity of this projectile will equal
, the horizontal velocity of this projectile will equal
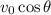 . The initial vertical velocity of this projectile will equal
. The initial vertical velocity of this projectile will equal
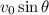 .
.
Assume that there's no air resistance on the projectile. The horizontal velocity of the projectile shall be constant. The range of this projectile will be the same as its displacement in the horizontal direction. That is:
Range = Horizontal Displacement = Horizontal Velocity × Time in the Air.
In the vertical direction, gravity causes the object to accelerate downwards at
 .
.
The vertical velocity on the projectile is zero at the vertex of its trajectory. The trajectory of the projectile is symmetric about the vertex. As a result, the projectile reaches the vertex at one-half the total time that the projectile is in the air.
In other words, if
 be the total time that the projectile stays in the air, it will reach the vertex of its trajectory at
be the total time that the projectile stays in the air, it will reach the vertex of its trajectory at
 . Also, it takes a time of
. Also, it takes a time of
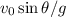 for the vertical velocity of the projectile to drop to zero. Since that's also the time it takes for the projectile to reach its vertex,
for the vertical velocity of the projectile to drop to zero. Since that's also the time it takes for the projectile to reach its vertex,
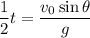 .
.
Solve for
 , the time that the projectile stays in the air:
, the time that the projectile stays in the air:
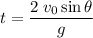 .
.
The range of the projectile launched at an angle of elevation
 and an initial velocity of
and an initial velocity of
 will thus equal:
will thus equal:
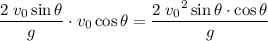 .
.
The range of a projectile launched at an initial velocity of
 will be
will be
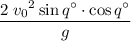 if
if
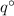 is the angle of elevation;
is the angle of elevation;
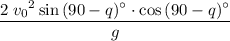 if
if
 is the angle of elevation.
is the angle of elevation.
Note that
 and
and
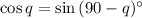 .
.
As a result,
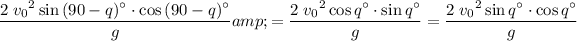 .
.
Hence the horizontal range of the projectile will be the same for angles of elevation
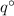 and
and
 .
.